Trumfové eso statistiky pro případ pandemie

Málokdo si pamatuje, co to je Bayesův teorém, přesto je doba pandemie přesně tím okamžikem, kdy není na škodu tento statistický koncept starý přes dvě stě let jemně oprášit. Podle Bayesova teorému lze určit pravděpodobnost nějakého jevu, který je závislý na tom, že se něco stalo předtím. Což je přesně případ náhodného lékařského testování.

Nositel Nobelovy ceny za ekonomii D. Kahneman uvádí pro ilustraci teorému asi nejvíce srozumitelný příklad. Ve městě jsou dvě taxikářské firmy. Ta větší jezdí se zelenými taxíky, ta menší s modrými. Celkem po městě jezdí 85% zelených a 15% modrých taxíků. Jeden z taxíků srazí chodce. Svědek, který nehodu viděl, tvrdí, že se jednalo o modrý taxík. Právníci obhajoby namítají, že bylo šero, a nechají svědka otestovat. Test za podobných světelných podmínek ukáže, že svědek v 80% případů rozpoznal barvu správně.

Je snadné se mýlit

Obžaloba říká: „Vidíte, 80%, to je klíčové svědectví.” Soudce souhlasí, neboť to na první pohled dává smysl. Jeho reakce je stejná jako u většiny lidí.

Ve skutečnosti je pravděpodobnost, že svědek správně označil modré auto, pouhých 41%, tedy poloviční. Obžalovaný tak musí doufat, že jeho obhajoba o Bayesově teorému už někdy slyšela.

Bayesův teorém měří pravděpodobnost nějakého jevu v závislosti na jevu druhém. V případě nehody je prvním jevem sražení chodce taxíkem nějaké barvy. To, co vidí svědek, je závislá událost a je závislá na tom, s jakou pravděpodobností to byl buď taxík zelený, nebo modrý. Podle celkových počtů zelených a modrých taxíků ve městě je pravděpodobnost 85%, že to byl zelený taxík, a 15%, že modrý. Je to logické, zelených taxíků je téměř šestkrát více. Beze svědka by byl výpočet hotov.

Zbývá již jen zakalkulovat fakt, že svědek viděl modré auto s 80% spolehlivostí? Jde to i bez vzorce.

Pravděpodobnost, že nehodu způsobilo modré auto, které svědek označí správně jako modré, je součin pravděpodobnosti výskytu modrého auta, to je 15%, a pravděpodobnosti správné odpovědi svědka, tedy 80%. Výsledek je 12%.

Stejným způsobem lze spočítat pravděpodobnosti pro zbylé tři kombinace barvy a správné či nesprávné odpovědi. Je to součin pravděpodobnosti výskytu taxíku určité barvy a spolehlivosti odhadu svědka, tedy 80%, že správně, a 20%, že se mýlí.

Je to matoucí

Ve 29 případech ze sta by podle známých pravděpodobností svědek řekl, že viděl modrý taxík. Ale pouze ve 12 případech by to bylo správné pozorování. V ostatních 17 případech by ve skutečnosti zelený taxík označil jako modrý. Proto je pravděpodobnost správné odpovědi v případě modrého taxíku pouze a jen 41%. Je to podíl správných odpovědí, 12, ku celkovému počtu případů, kdy řekne, že to bylo modré auto.

Toto je základní matoucí prvek Bayesova teorému, který způsobí, že intuitivní odhady pravděpodobnosti selhávají. Celková pravděpodobnost je dramaticky ovlivněna pravděpodobností prvního jevu, v tomto případě celkovými počty taxíků ve městě. Spolehlivost odhadu svědka je méně důležitá, protože závisí na tom, co se stalo předtím.

Kdyby ve zcela identickém případě svědek řekl, že na vině je zelený taxík, byla by pravděpodobnost, že odpověděl správně, 96%.

A k čemu je to dobré? 

Je dobré tušit, že něco takového existuje, zvláště v době pandemie. Nejčastější a nejcitovanější využití podmíněné pravděpodobnosti a Bayesova teorému je totiž v lékařském testování.

U každého lékařského testu jsou stanoveny ukazatele, které měří s jakou pravděpodobností vyjde test jako negativní, i když je testovaná choroba přítomna, a naopak s jakou pravděpodobností vyjde test pozitivní, i když je testovaný člověk zdráv. Spolehlivost používaného testu je určena počtem falešně pozitivních a falešně negativních výsledků.

Spolehlivost daného testu na přítomnost choroby se měří jeho porovnáním proti výsledkům nějakého testu, který je považován pro danou chorobu za takzvaný zlatý standard, protože je nejlepší. Pouze pro ilustraci a extrémně laicky řečeno by se spolehlivost testu na zlomeninu končetiny, který provádí lékař pohledem a ohmatáním končetiny, měřila oproti výsledkům rentgenu.

Velmi překvapivý výsledek

Pravděpodobnost výskytu choroby při náhodném testování je určena Bayesovým teorémem. Jedná se o úplně stejný případ jako zelený versus modrý taxík s identickým výpočtem. První událostí je výběr testovaného vzorku lidí, druhou událostí provedení testu.

Výsledek je stejně překvapivý. Je-li nakažen jeden člověk z tisíce a test vykazuje 1% falešně pozitivních nálezů, má pozitivní nález malou vypovídací hodnotu.

Je vybráno náhodně 1 000 lidí. Protože obecný výskyt choroby v populaci je jeden z tisíce, je jeden z nich nakažen. Všichni jsou otestováni. 1% falešně pozitivních nálezů znamená, že z tisíce testovaných lidí test vykáže deset falešně pozitivních nálezů. A samozřejmě také najde toho jednoho nakaženého.

Testovací laboratoř má na stole jedenáct pozitivních nálezů, z nichž pouze jeden znamená, že je daný člověk skutečně nakažen. Pravděpodobnost správného výsledku testu je jedna ku jedenácti, což je méně než 10%.

Procento falešně pozitivních nálezů u antigenních testů na koronovirus udává vláda jako „velmi nízké”. Testovací laboratoře uvádějí hodnotu nižší než 1%. Výskyt nově nakažených koronavirem v populaci byl v prvním týdnu v listopadu zhruba ve výši pět nakažených na tisíc obyvatel, tedy 0.5%.

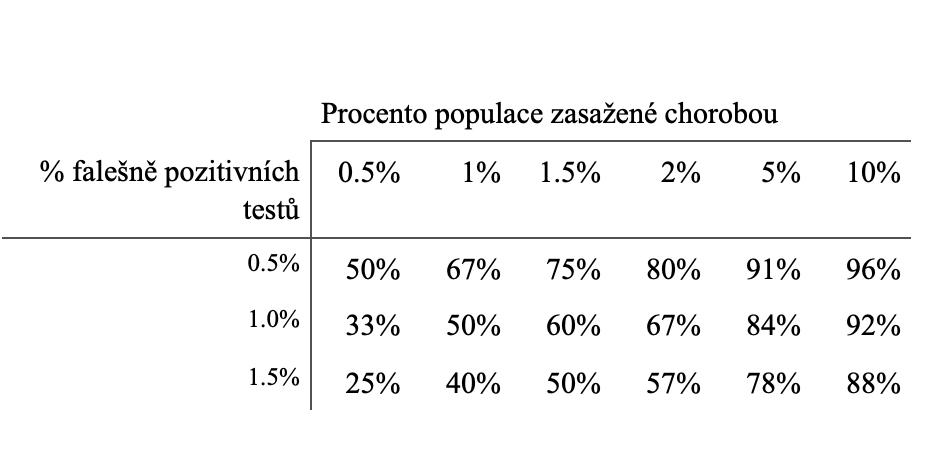
Pravděpodobnost, že pozitivní test skutečně potvrzuje přítomnost nějaké choroby, je uvedena v tabulce níže. A to pro několik kombinací spolehlivosti testu a obecného výskytu choroby v populaci.